Imagine you developed a new system (for example a car or some other machine) and tested it under operation for $10^4$ hours. During this testing period, the system operated without fault. What conclusions can we draw from such a test with respect to the reliability of the system? Using a Poisson process to model the failure of the system under operation and a Bayesian post-processing strategy allows us to answer that question.
An unbiased point estimate for the rate $\lambda$ of a Poisson process is $x/t$, with $x$ the number of observed occurrences within $t$. However, for small $\lambda$ or for short observation periods $t$, it can happen that $x$ is zero. In fact, $x$ being zero is usually desired when observing failures of safety-critical systems. However, declaring $\lambda$ as zero based on such an observation is clearly unsatisfactory for such systems.
Using a Bayesian strategy to quantify the uncertainty about the rate of a Poisson process, the uncertainty about $\lambda$ can be expressed analytically. This allows us to derive upper credible intervals for $\lambda$, even if $x$ is zero. These credible intervals are ideally suited for engineering applications, as they are actually on the conservative side.
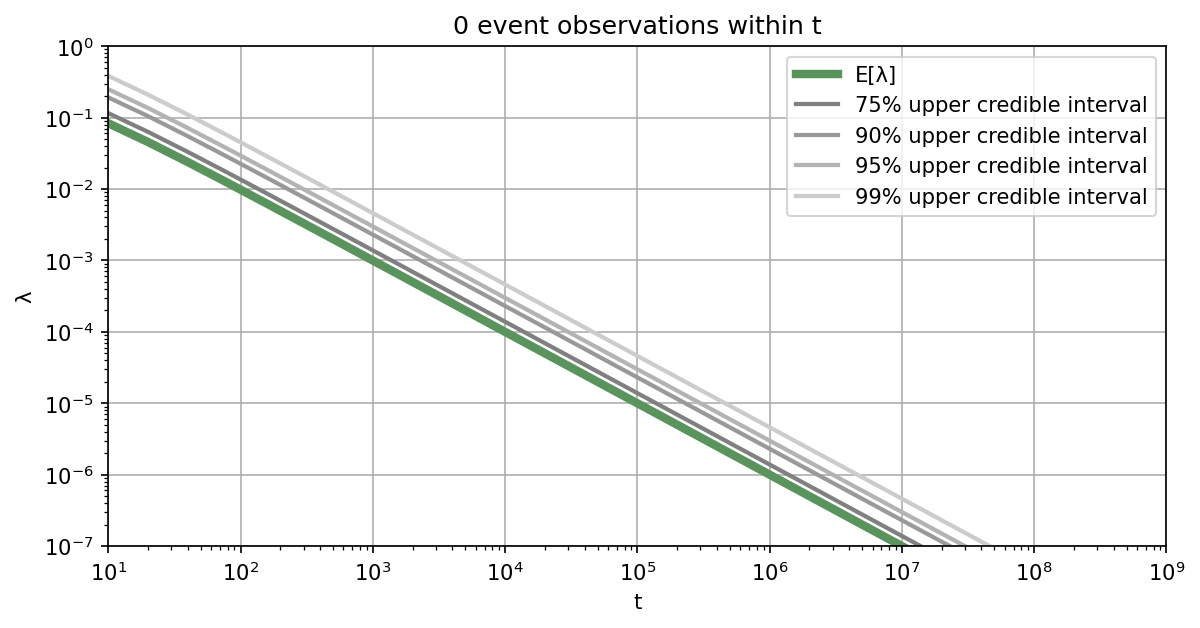
In the figure above, upper credible intervals and the mean value for lambda are shown as a function of the observation time, assuming $x=0$. Alternatively, you can use our Online Tool for the post-processing of a Poisson process.
Illustrative example: For example, if $x$ is still zero after observing the Poisson process for $10^4$ hours, the expected value of $\lambda$ is $1.0\times10^{-4}$ events per hour, the $95\%$ upper credible interval for $\lambda$ is $3.0\times10^{-4}$ events per hour and the $99\%$ upper credible interval is $4.6\times 10^{-4}$ events per hour. ■
+49 (0)89 21709083
