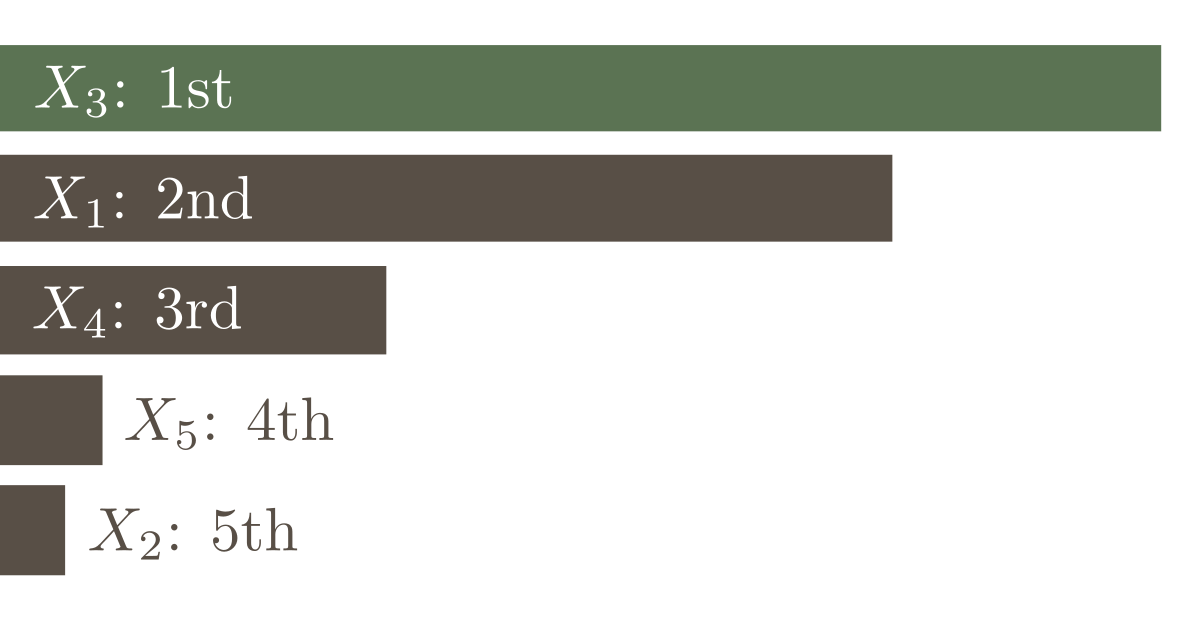
In factor prioritization, the purpose of a sensitivity analysis is to establish a ranking of the input parameters according to their importance on the model output. However, it is important to be aware that "most important" can mean different things in different settings. Therefore, before applying any sensitivity measure for factor prioritization, it is important to clearly define what 'most important' means in your setting.
Factor prioritization in a variance-based sensitivity analysis
An often applied interpretation of "importance" is to define the "most influential model input parameter" as the one that on average, once fixed, would cause the largest reduction in variance [Saltelli, 2008]. The averaging is performed over the distribution of the respective model input parameter. Thus, we search a sensitivity measure that is proportional to the first-order effect $V_i= \operatorname{Var}_{X_i}\left[ \operatorname{E}_{\mathbf{X}_{\sim i}}\left[Y|X_i\right] \right]$. This is exactly how the first-order sensitivity indices $S_i$ are defined:
$$
S_i = \frac{V_i}{\operatorname{Var}[Y]} = \frac{\operatorname{Var}_{X_i}\left[ \operatorname{E}_{\mathbf{X}_{\sim i}}\left[Y|X_i\right] \right]}{\operatorname{Var}[Y]} \;.
$$
Note that in the above-stated interpretation of "importance", it is assumed that the model input parameters have a true, albeit unknown value. Thus, all parameter uncertainties are purely epistemic. If the uncertainties about a model input parameter contain at least an aleatory component, the stated interpretation loses its practical usefulness. A potential remedy is to clearly separate epistemic and aleatoric uncertainties in the probabilistic model and to take only the epistemic uncertainties into account for factor prioritization.
Another important observation is that in the interpretation stated above it is implicitly assumed that all experiments required to uniquely identify the model parameters have exactly the same cost. This is usually not the case in practical applications.
The first-order sensitivity is a measure for the expected relative gain of identifying the "true" value of a parameter. Whether or not the so-obtained ranking is truly optimal can only be determined in hindsight when the "true" values of all parameters are known. It is also unknown in advance how much the variance can truly be reduced when learning the "true" value of a parameter — in advance, we can only estimate what to expect by identifying the "truth".
References
[Saltelli, 2008] Saltelli, Andrea, et al. Global sensitivity analysis: the primer. John Wiley & Sons, 2008.
+49 (0)89 21709083
