What are the first-order sensitivity indices?

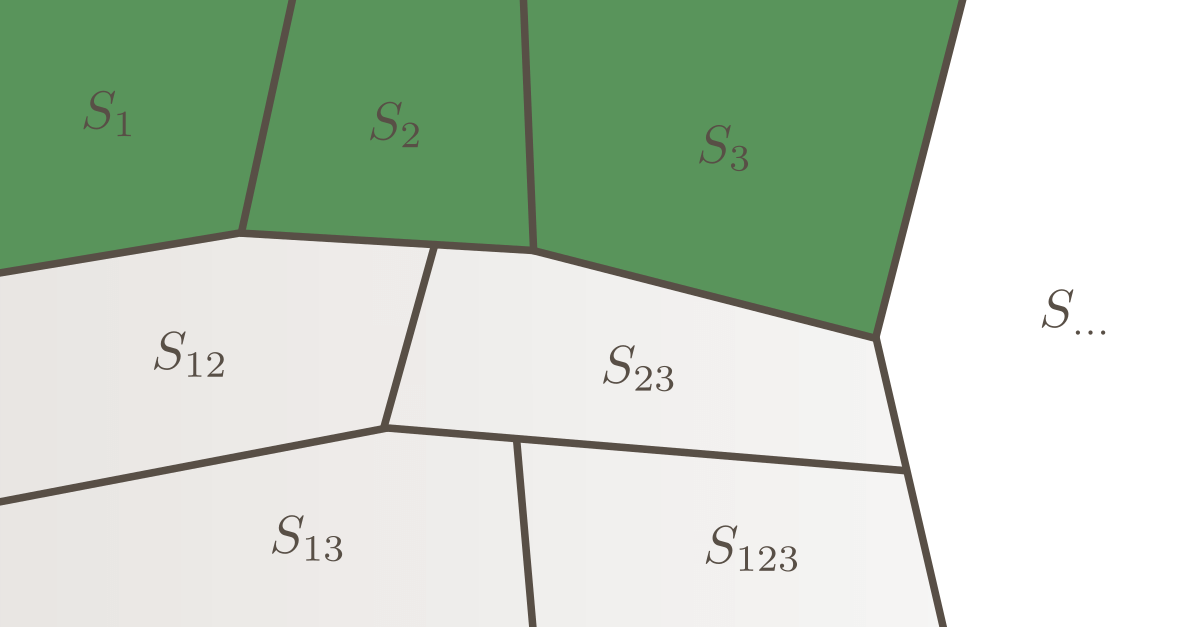
You have a stochastic model $Y(\mathbf{X})$ that is driven by the vector $\mathbf{X}$ of uncertain model input parameters. If you need to establish a ranking of the input parameters according to their importance on the model output, the first-order sensitivity indices are a commonly applied sensitivity measure for that purpose.

Definition

The "first-order sensitivity index" is also referred to as the "first-order Sobol index" or "main effect index". The first-order sensitivity index $S_i$ associated with model input parameter $X_i$ quantifies the effect of varying $X_i$ alone, averaged over the contributions of the other input parameters $\mathbf{X}_{-i}$, with $\mathbf{X}_{-i} = \left[X_1,\ldots,X_{i-1},X_{i+1},\ldots,X_M\right]$. $S_i$ is defined as the first-order effect $V_i$ from the variance decomposition divided by the variance $\operatorname{Var}[Y]$ of the model output $Y$:
$$
S_i = \frac{V_i}{\operatorname{Var}[Y]} = \frac{\operatorname{Var}_{X_i}\left[ \operatorname{E}_{\mathbf{X}_{\sim i}}\left[Y|X_i\right] \right]}{\operatorname{Var}[Y]} \;,
$$ where $\operatorname{E}_{\mathbf{X}_{\sim i}}\left[Y|X_i\right]$ is the expected value of the model output with respect to all input variables except $X_i$ (which is fixed).

Sum of Sobol-based sensitivity indices

Note that due to the link between the Sobol-based sensitivity indices and the variance decomposition, it must hold that:
$$
\sum_{i=1}^M S_i + \sum_{i<j}^M S_{ij} + \ldots + S_{12\ldots M} = 1\;,
$$ where a higher-order index $S_\mathbf{a}$ is defined as:
$$
S_\mathbf{a} = \frac{V_\mathbf{a}}{\operatorname{Var}[Y]}\;.
$$

Thus, $1-\sum_{i=1}^M S_i$ quantifies the fraction of the model output $Y$ that cannot be explained by first-order effects. Note that for additive models we have by definition: $\sum_{i=1}^M S_i=1$. Correspondingly, for non-additive models, we have $\sum_{i=1}^M S_i<1$.

Interpretation of first-order sensitivity indices

The first-order sensitivity indices are well suited for factor prioritization; i.e., to establish a ranking of the input parameters according to their importance on the model output. More specifically, the first-order sensitivity indices identify the model parameters that on average, once fixed, would cause the largest reduction in variance [Saltelli, 2008].

Illustrative example

The problem

We model fatigue deterioration by the Palmgren-Miner rule with constant stress ranges in all cycles. The fatigue damage $D$ is evaluated as: $$
D = n\cdot\frac{\Delta S^m}{K} \,.
$$ The parameters in the equation above are:

• $n$: the number of stress cycles; is modeled as deterministic and set to $10^7$.
• $m$: a material parameter; is modeled as deterministic and set to $3.0$. 
• $\Delta S$: the stress range (which is constant in all cycles); is modeled as a log-Normal distribution with mean $50 N/s^2$ and standard deviation $10 N/s^2$. 
• $K$: a material parameter; is modeled as a log-Normal distribution with mean $4.5\cdot 10^{12} N^3/s^6$ and standard deviation $2.25\cdot 10^{12} N^3/s^6$.

Thus, the fatigue damage depends on the uncertain model parameters $\Delta S$ and $K$. 

The question to answer

We perform a sensitivity analysis in order to answer the following question: Which model parameter would (on average) cause the largest reduction in variance if we could determine its value exactly (i.e., fully eliminate the uncertainty of the associated parameter)?

The solution

The first-order sensitivity indices are $$
S_{\Delta S} = 0.53 \,,
$$ and $$
S_{K} = 0.32 \,.
$$

The uncertain model parameter $\Delta S$ is the most influential; i.e., $\Delta S$ would on average cause the largest reduction in variance if its value could be fixed. However, also the uncertain model parameter $K$ has a notable influence.

The fraction of the model output that cannot be explained by first-order effects is $$
1-S_{\Delta S} -S_{K}=1-0.53-0.32=0.15\,.
$$ ■

References

[Saltelli, 2008] Saltelli, Andrea, et al. Global sensitivity analysis: the primer. John Wiley & Sons, 2008.