One way to simplify a probabilistic model is to reduce the number of probabilistic model parameters (i.e., the ones with uncertain values). In order to do so, we need to know which model parameters have no or only negligible impact on the model output. The total-effect sensitivity indices are ideally suited for that task.
The total-effect sensitivity index $S_i^T$ of model input parameter $X_i$ quantifies the combined effect of $X_i$ with other model input parameters on the variance of the model output.
Definition
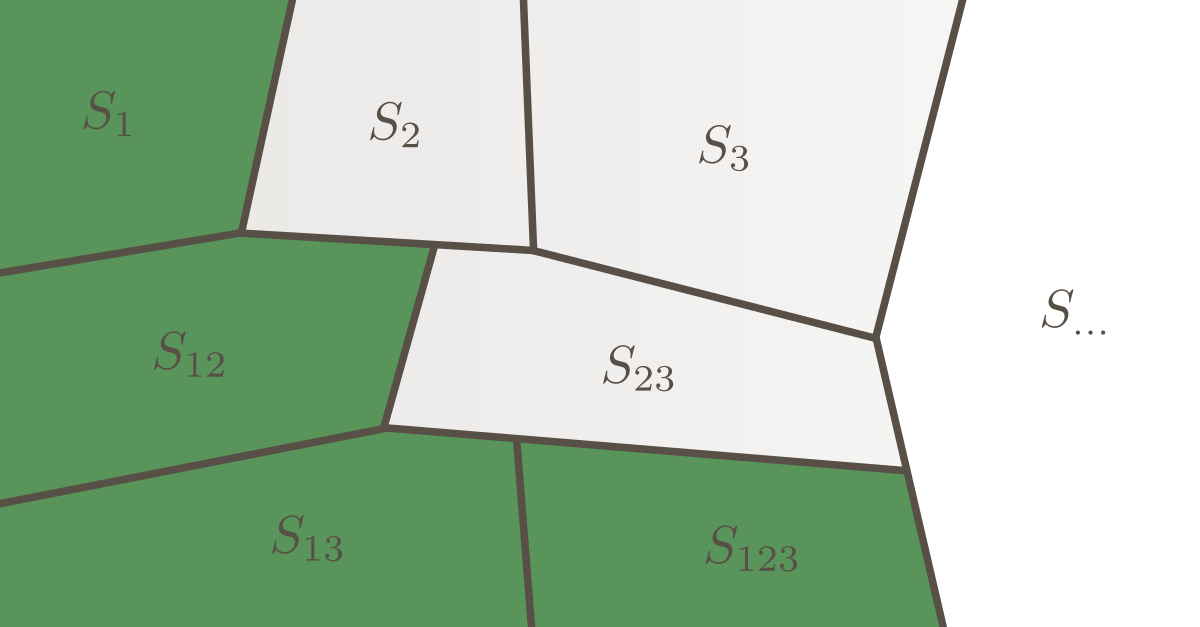
Let's recall that the sum of all sensitivity indices of all orders equals one:
$$
\sum_{i=1}^M S_i + \sum_{i<j}^M S_{ij} + \ldots + S_{12\ldots M} = 1\;,
$$ where the sensitivity index $S_\mathbf{a}$ is defined as:
$$
S_\mathbf{a} = \frac{V_\mathbf{a}}{\operatorname{Var}[Y]}\;,
$$
with $V_\mathbf{a}$ as the associated term from the variance decomposition.
The total-effect sensitivity index $S_i^T$ is defined as the sum of the sensitivity indices of all orders involving the $i$th model input parameter. For example, $S_1^T$ of a model with three parameters is defined as $S_1^T = S_1 + S_{12}+S_{13} +S_{123}$. However, the number $N$ of terms to evaluate $S_i^T$ grows exponentially with the number $M$ of model input parameters; i.e., $N = 2^M-1$. Alternatively, $S_i^T$ can also be evaluated as:
$$
S_i^T = \frac{\operatorname{E}_{\mathbf{X}_{\sim i}}\left[\operatorname{Var}_{X_i}\left[Y|\mathbf{X}_{\sim i}\right]\right]}{\operatorname{Var}[Y]}\;.
$$
Note that for additive models we have $S_i^T = S_i$. However, in general, $\sum_{i=1}^M S_i^T \ge 1$.
Interpretation of total-effect sensitivity indices
The total-effect sensitivity indices are well suited for factor fixing; i.e., to identify input parameters that are of minor importance with respect to the model output.
Computation
An obstacle in the practical application of the total-effect sensitivity indices is that (unlike the first-order sensitivity indices) they cannot be evaluated in a computationally cheap post-processing step (of a conducted Monte Carlo simulation). Especially for models with many parameters and/or computationally challenging models, the computational cost of computing the total-effect sensitivity indices is often prohibitive.
A Monte Carlo based approach to estimate $S_i^T$ is provided in [Saltelli etal., 2010].
Illustrative example
The following example is taken from [Straub, 2019].
The problem
We have the model $Y$: $$
Y = A_1\cdot X_1 + A_2 \cdot X_2\,,
$$ which is driven by the uncertain model parameters $X_1$, $X_2$, $A_1$ and $A_2$ that are modeled probabilistically. Both $X_1$ and $X_2$ represent random effects that cannot be controlled. Both $A_1$ and $A_2$ can be interpreted as model coefficients that are not known with certainty – and therefore modeled probabilistically.
The distributions of the probabilistic (i.e., uncertain) model parameters are:
- Both $X_1$ and $X_2$ are modeled by a standard Normal distribution.
- $A_1$ is modeled as a beta distribution with a mean of $0.7$ and a standard deviation of $0.2$.
- $A_2$ is modeled as a beta distribution with a mean of $0.3$ and a standard deviation of $0.1$.
The question to answer
We perform a sensitivity analysis in order to answer the following question: Exist uncertain model parameters that have a negligible impact on $Y$ and can, therefore, be replaced by a deterministic variable (i.e., with a fixed value)?
The Answer
The total-effect sensitivity indices can be computed as: $S_{X_1}^T \approx 0.84$, $S_{X_2}^T \approx 0.16$, $S_{A_1}^T \approx 0.06$ and $S_{A_2}^T \approx 0.01$. Thus, all parameters have a measurable impact on the variance of $Y$. The parameter with the least influence is $A_2$. ■
References
[Saltelli etal., 2010] Saltelli, A., P. Annoni, I. Azzini, F. Campolongo, M. Ratto, and S. Tarantola: Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Computer Physics Communications 181(2), 259–270, 2010.
[Straub, 2020] Straub, Daniel: Lecture Notes in Engineering Risk Analysis. Technische Universität München, 2020.
