For how long do you need to observe a Poisson process to ensure that its rate is smaller than a specified threshold?

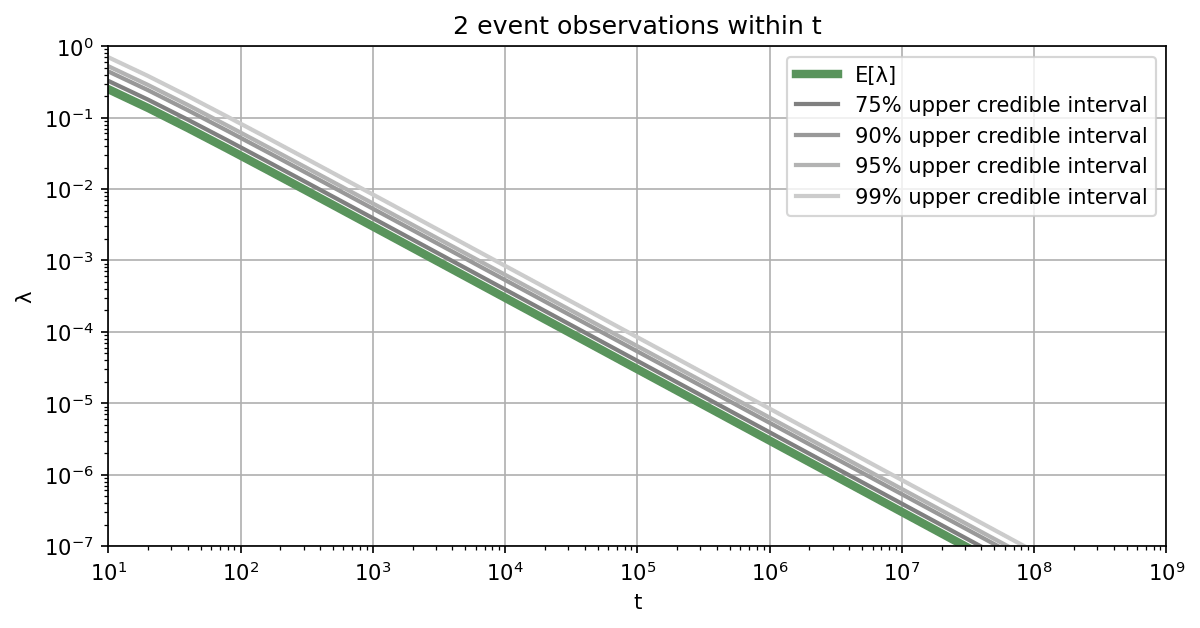
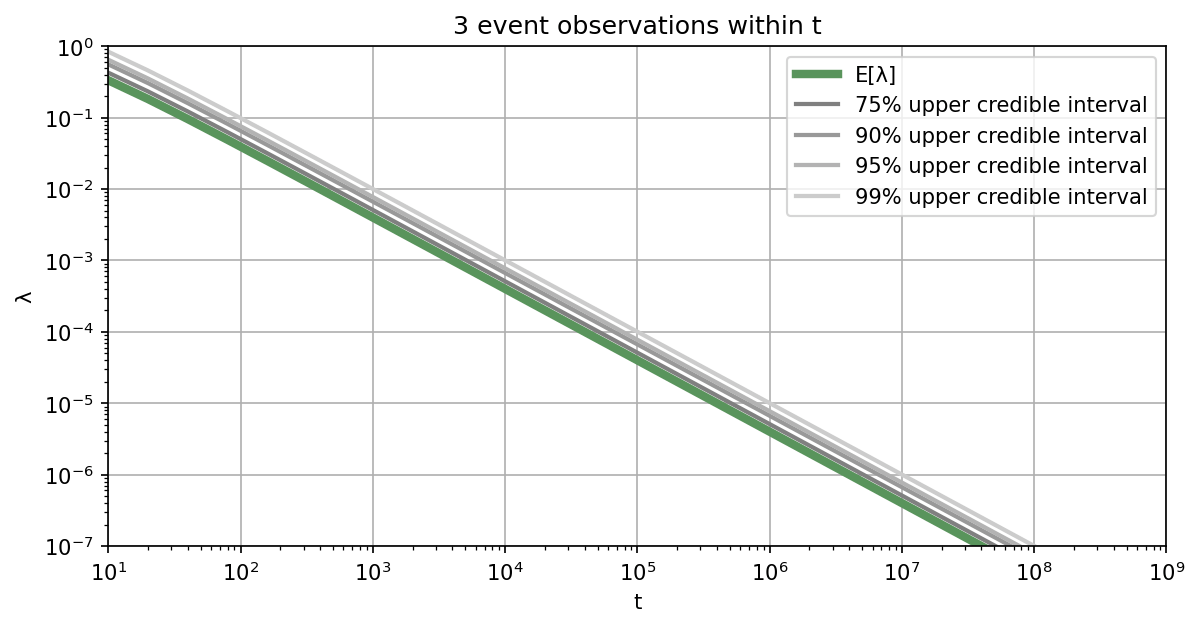
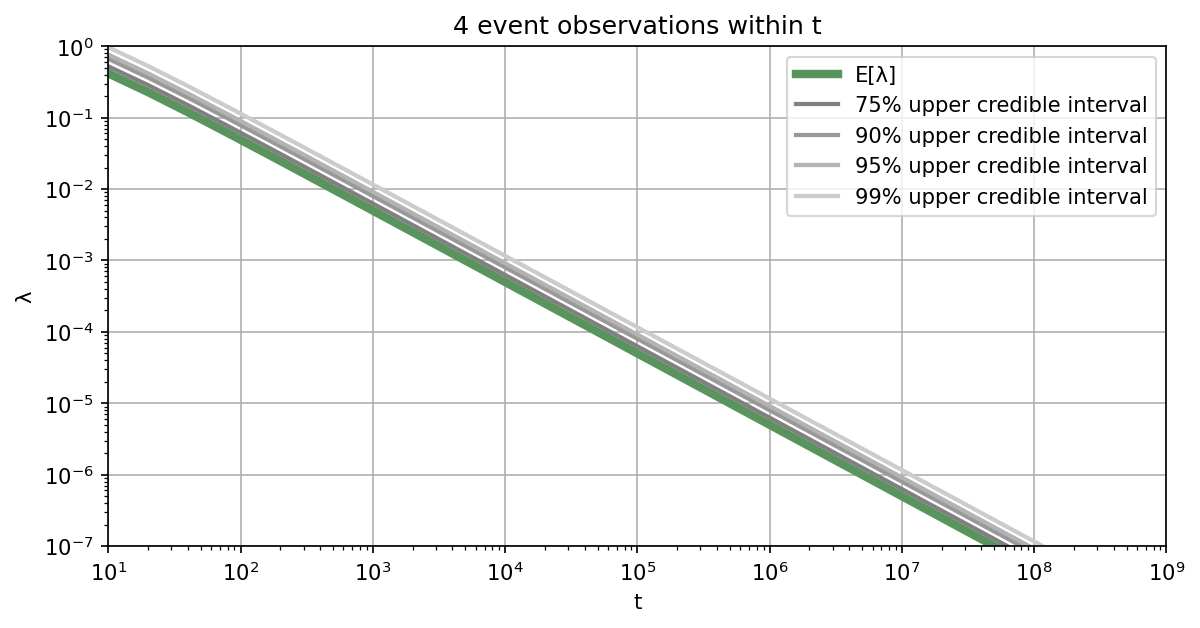
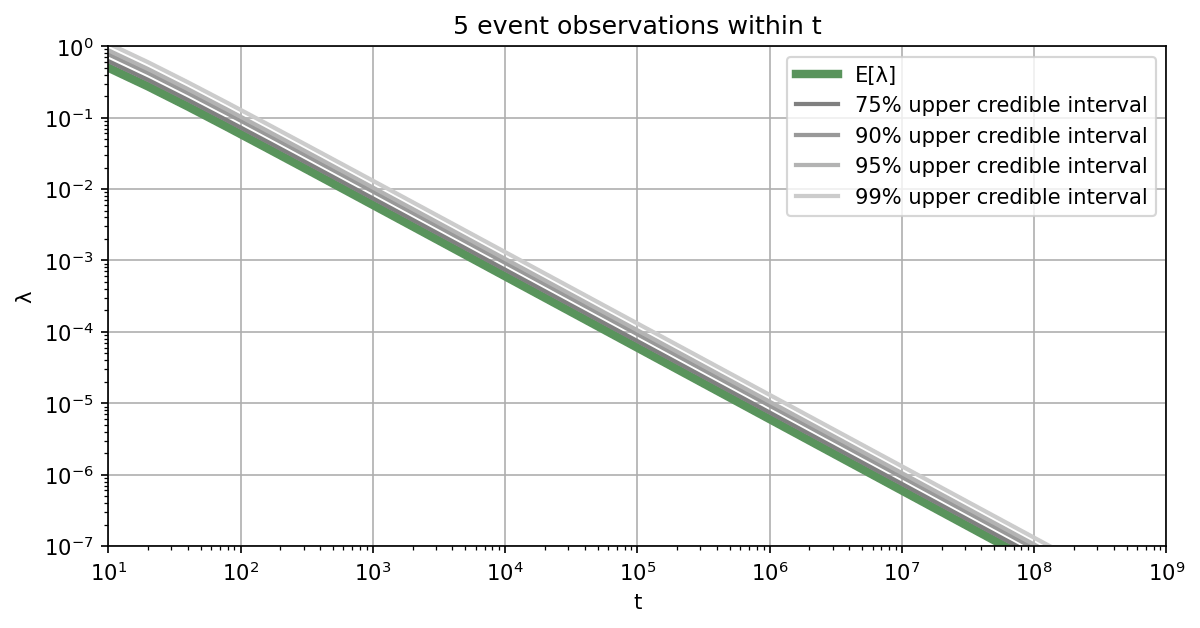
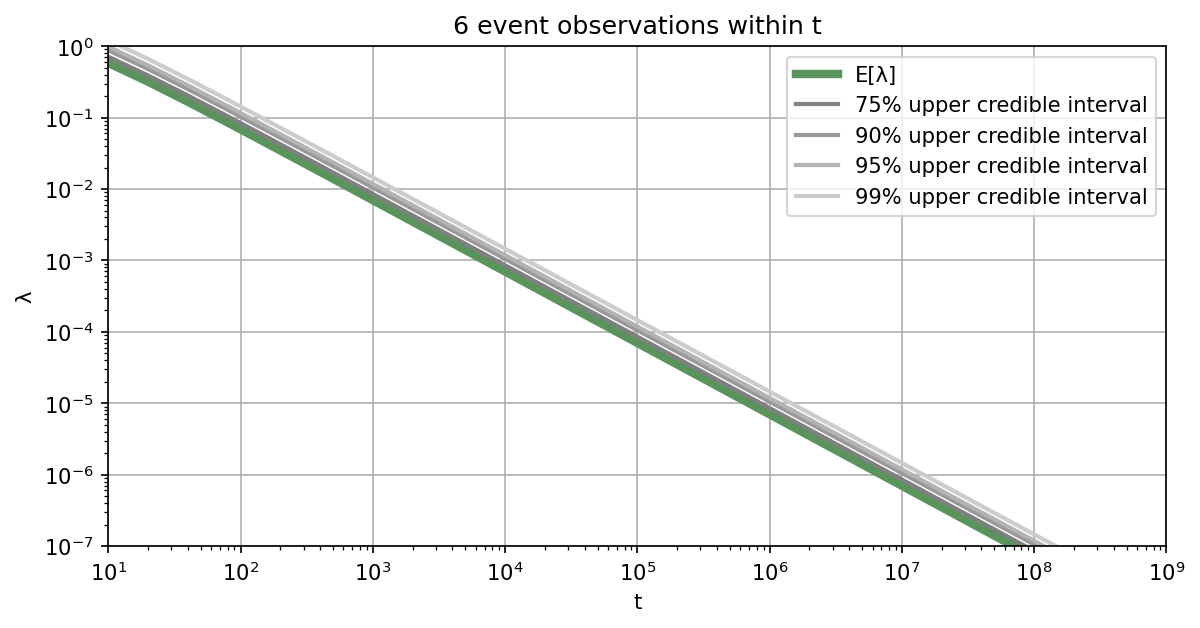
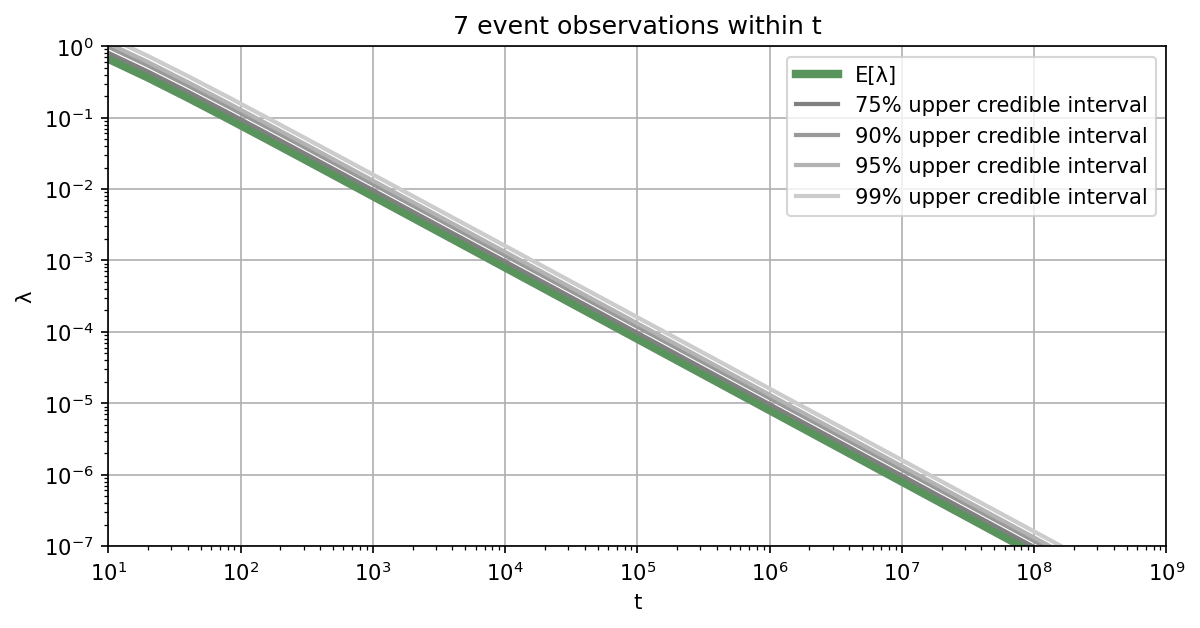
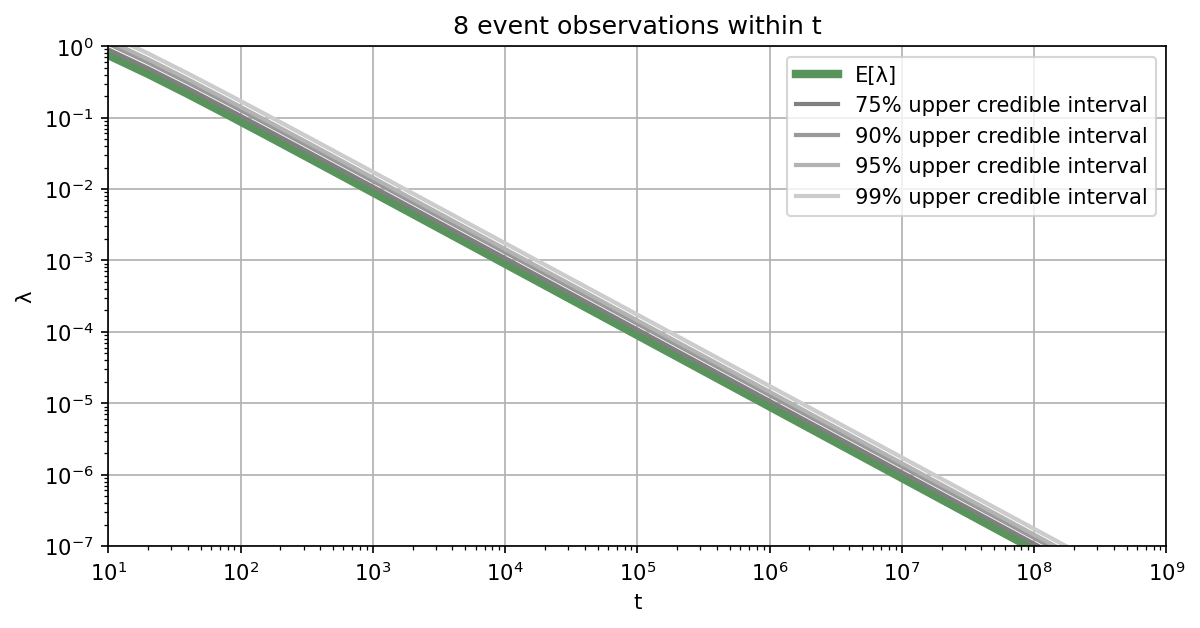
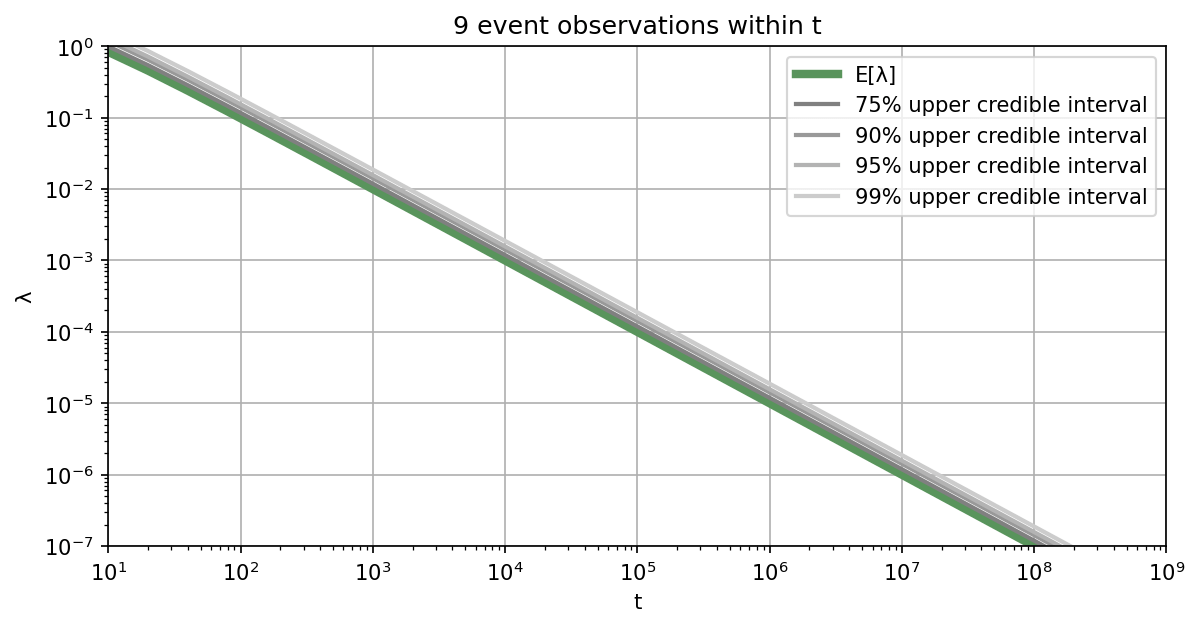
Let's assume you are interested in learning the failure rate of a safety-critical system, where failures of this system can be represented by a Poisson process. For how long do you need to monitor the system, in order to demonstrate that the failure rate is below a specified threshold? Of course, this depends on the aspired credibility level and also on how many failures will occur within the observation period.

Below we provide a list of plots that can be used to determine how long the system of interest needs to be monitored to reach the specified safety level with aspired credibility. Alternatively, you can also use our Online Tool for the Poisson testing period. If you want to be $95\%$ sure that the rate is below the required threshold, you should work with the $95\%$ upper credible interval. 

Illustrative example: For example, if the target threshold value is $10^{-4}$ failures per hour and assuming that no failures will happen during the monitoring phase, the system needs to be monitored for at least $3\times10^4$ hours to reach a credibility of $95\%$. If you assume that one failure will happen during the monitoring, you need to monitor the system already for $4.8\times10^4$ hours. In case you assume 10 failures, you need to monitor for $1.7\times10^5$ hours to achieve a credibility of $95\%$. ■