What is the difference between credible and confidence intervals?

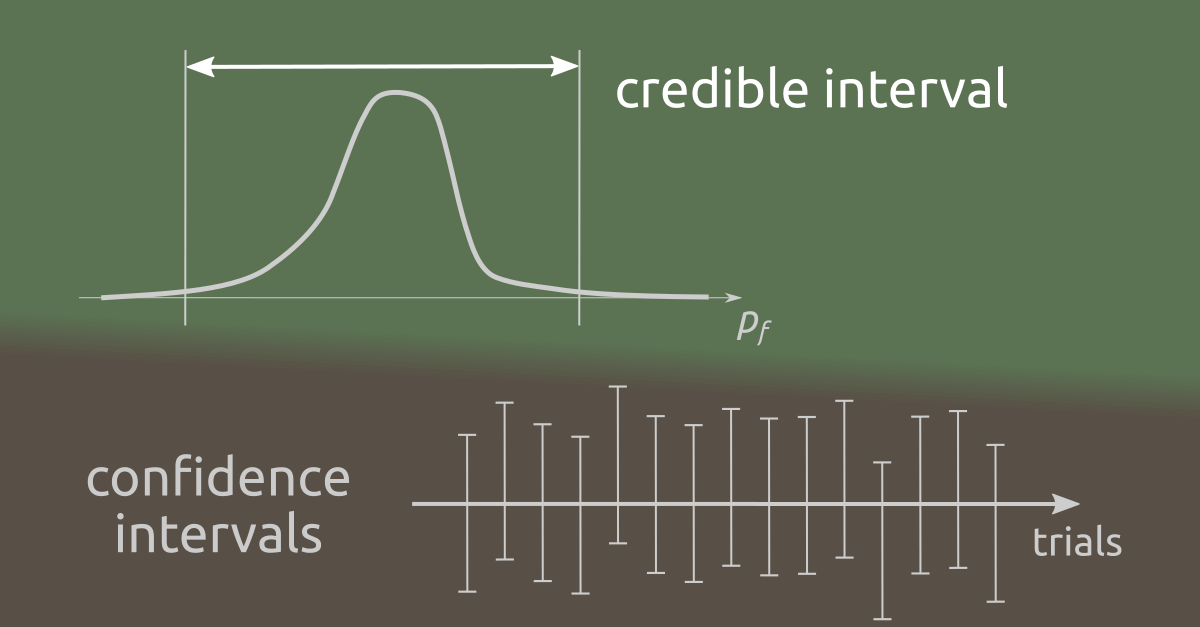
Let's assume we conducted a stochastic simulation run to estimate an unknown underlying quantity $p$. For example, the simulation run can be a Monte Carlo simulation in the context of structural reliability and the unknown underlying quantity $p$ could be the probability of failure. Credible intervals express our belief that $p$ is contained within the interval conditional on the conducted simulation run; e.g. with a probability of $95%$ we believe that $p$ is within the interval conditional on the conducted simulation run. Confidence intervals state that if the simulation is repeated infinitely many times and for each simulation run the corresponding $95%$ confidence interval for $p$ is evaluated, then the $p$ is actually contained within at least $95%$ of all obtained intervals. More generally, the notion of credible intervals is mainly used within a Bayesian context, whereas confidence intervals are based on frequentist statistics.

In the Bayesian viewpoint, the uncertainty about $p$ is expressed by a random variable $P$.  In this context, the outcome of a stochastic simulation run is used to update a prior belief on the distribution of $P$ using Bayes’ rule. From the so obtained posterior distribution, credible intervals can be evaluated based on quantile values. Thus, there is always a proper distribution behind a credible interval.

This is not necessarily the case for confidence intervals. Thus, it is wrong to interpret a $95%$ confidence interval as if it states that there is at least a $95%$ probability that $p$ is contained within a specific interval. By definition, it is merely required that $95%$ of all obtained intervals contain $p$. This non-trivial interpretation of confidence intervals is one of the reasons why confidence intervals are often used as if they were credible intervals.

Moreover, in engineering, we can typically afford to conduct a stochastic simulation run only once. If we could run it multiple times, it would usually be better to increase the computational cost of a single simulation run (e.g., by increasing the number of samples). Thus, confidence intervals are of little use for engineering decision-making. Contrary to that, making statements conditional on a single simulation run is exactly the scope of credible intervals.