How is the reliability index linked to the probability of failure?

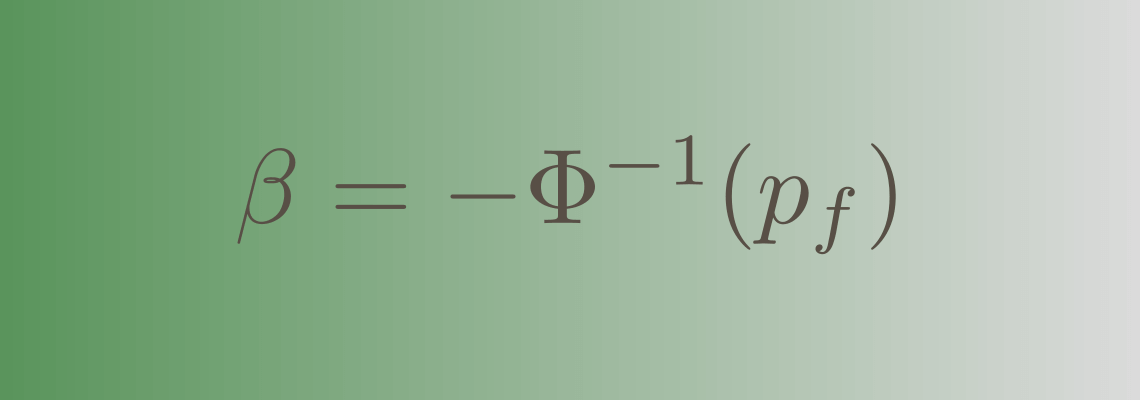
The probability of failure $p_f$ is a measure for the degree of safety (i.e., the reliability) of the investigated structure. The smaller the probability of failure, the larger the reliability. The probability of failure $p_f$ usually ranges from $10^{−1}$ to $10^{−7}$ [Kiureghian, 1989]. An often more convenient measure to express the reliability of the investigated structure is provided by the reliability index, which increases with increasing reliability. The generalized reliability index $\beta$ is defined as [Ditlevsen, 1979; Ditlevsen and Madsen, 2007, Chapter 6]:
$$
\beta = −\Phi^{-1}\left(p_f\right)\;,
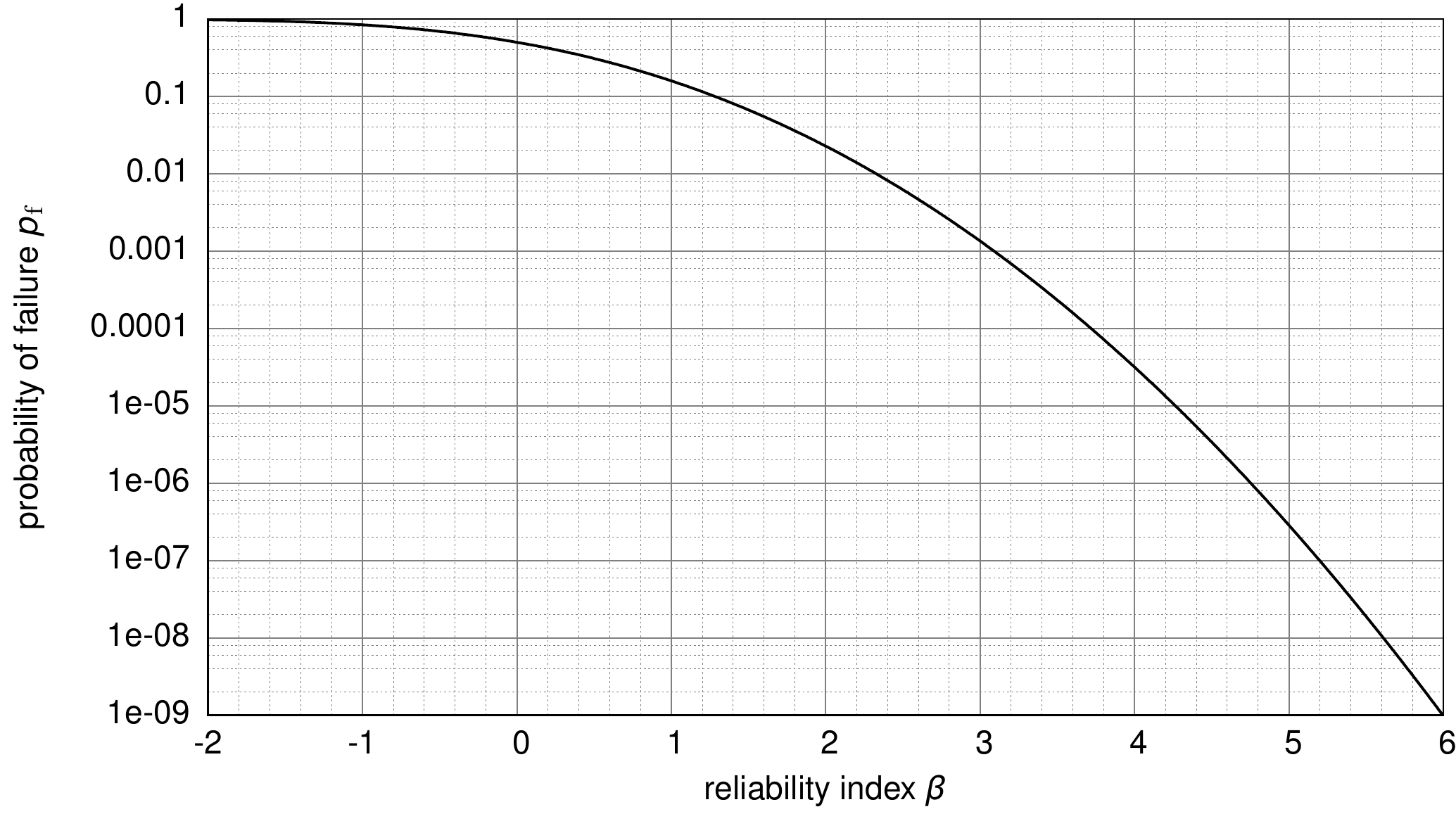
$$ where $\Phi^{-1}(\cdot)$ is the inverse of the CDF of the standard Normal distribution. The reliability index $\beta$ increases with decreasing probability of failure; i.e., the larger $\beta$ the larger the reliability of the investigated structure. For $p_f = 10^{−1}$, the reliability index is approximately $1$, and for $p_f = 10^{−7}$, the reliability index is approximately $5$. The relation between the reliability index $\beta$ and the probability of failure $p_f$ is illustrated in the figure below.

Note that the above definition of the generalized reliability index differs from the FORM reliability index $\beta_\mathrm{FORM}$, which (i) measures the distance of the design point from the origin in standard Normal space and (ii) is the reliability index associated with the linearized limit-state function at the design point.

References

[Kiureghian, 1989] Kiureghian, A. D.: Measures of structural safety under imperfect states of knowledge. Journal
of Structural Engineering, 115(5):1119–1140, 1989.

[Ditlevsen, 1979] Ditlevsen, O.: Generalized second moment reliability index. Journal of Structural Mechanics,
7(4):435–451, 1979.

[Ditlevsen and Madsen, 2007] Ditlevsen, O. and Madsen, H. O.: Structural reliability methods. Technical University of
Denmark, 2007.