What is FORM?

The first-order reliability method (FORM) is a numerical structural reliability analysis method that approximates the probability of failure by linearizing the limit state function around the design point. Thus, in FORM, first, the design point needs to be identified, which requires the numerical solution of a constraint optimization problem. Thereafter, a first-order approximation of the probability of failure can be obtained by a linearization of the limit state function. The linearization requires the limit state function to be differentiable at the design point. Additionally, most commonly used optimization algorithms require the limit state function to be differentiable in the entire domain of the input parameter space $\mathbf{X}$. The standard variant of FORM also requires that the structural reliability problem is characterized by a single design point.

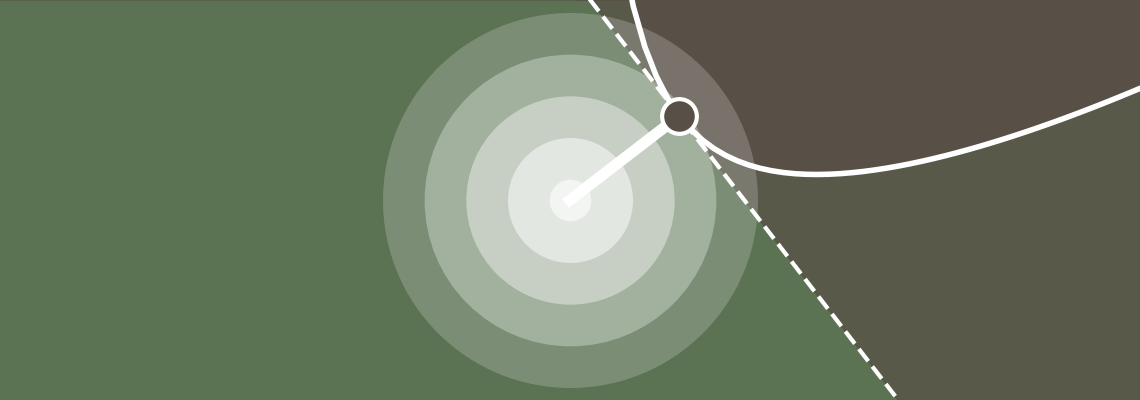
Design point and probability of failure

The vector $\mathbf{u}^*$ pointing from the origin in standard Normal space to the coordinates of the design point in standard Normal space is orthogonal to the transformation of the limit state function in standard Normal space. Let $\beta_\mathrm{FORM}$ denote the length of this vector. It can be shown that the first-order approximation of the probability of failure can be expressed as:
$$
p_{f,\mathrm{FORM}} = \Phi\left(-\beta_\mathrm{FORM}\right)\,,
$$ where $\Phi(\cdot)$ denotes the cumulative distribution function (CDF) of the standard Normal distribution. $\beta_\mathrm{FORM}$ is also referred to as the FORM reliability index.

The property that $\mathbf{u}^*$ is orthogonal to the limit state function can also be exploited for sensitivity analysis.

Accuracy and computational cost

If FORM can be applied, an estimate of the probability of failure can be obtained with a relatively small number of calls of the limit state function, compared to sampling-based reliability methods. This especially holds true if the problem is low-dimensional; i.e., if the number of uncertain model parameters is small. For problems with a large number of uncertain model parameters, the numerical performance is negatively affected by the finite difference step required by most optimization algorithms (as in practice derivatives are usually not directly available as a by-product of the evaluation of the limit state function). Nevertheless, also in higher dimensional problems, FORM is usually able to obtain an estimate of the probability of failure with a smaller number of limit state function calls than sampling-based reliability methods.

In practice, the FORM estimate is often surprisingly close to the actual probability of failure. This is because, for systems with a small probability of failure, most of the probability mass in the failure domain is actually assembled in the vicinity of the design point. Thus, the first-order approximation usually is reasonably close to the truth even if the limit state function is non-linear.

If the limit state function is computationally expensive to evaluate, FORM with a subsequent run of line-sampling (with a very small number of samples; e.g., 10 to 100) provides often very accurate estimates of the probability of failure with a minimum number of limit state function calls.