Structural reliability analysis aims at evaluating the probability of failure of a structure or system of interest. In this context, failure is defined as the structure/system being in an undesired state, e.g.: admissible stresses are exceeded, the stability of a structure is no longer maintained, or water levels in a river that exceed a certain threshold will result in a flood event. Let such an undesired system response be denoted as proposition $\mathcal{F}$, where the probability of failure $p_f$ is defined as the probability that $\mathcal{F}$ occurs, i.e., $p_f = \Pr\left(\mathcal{F}\right)$.
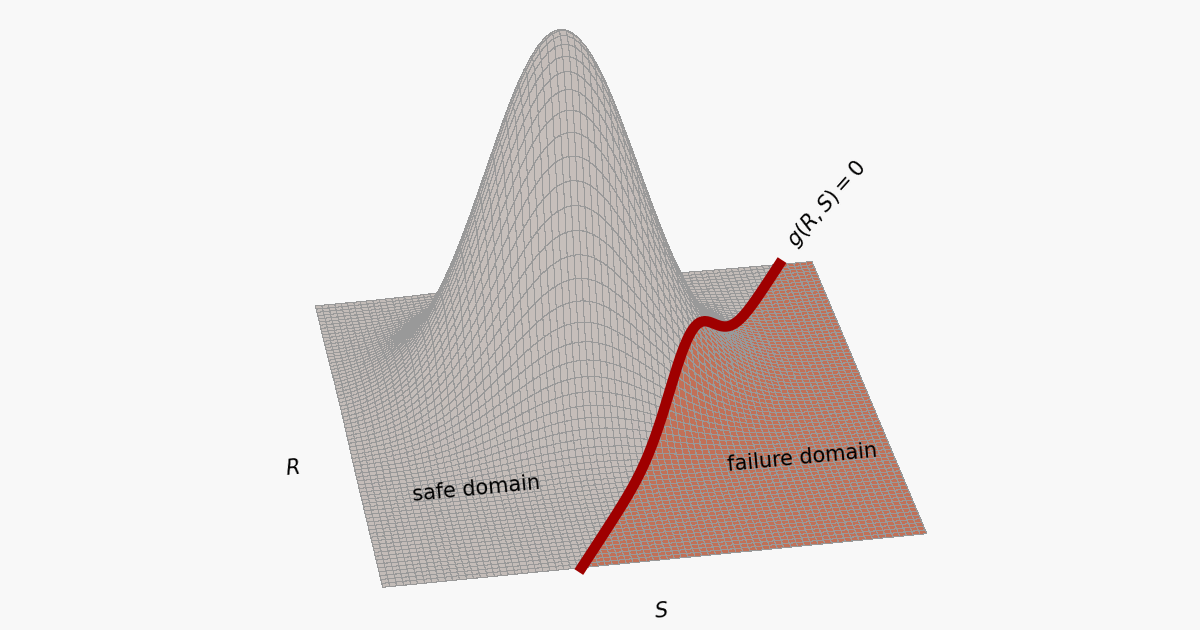
Typically, the response of the system of interest needs to be approximated by a model $\mathcal{M}$. For example, the response can be approximated by a simple analytical expression or by a complex finite element model. Let $\mathbf{X}$ be the $M$-dimensional stochastic vector of uncertain model parameters for $\mathcal{M}$. Furthermore, let $\Omega \subseteq \mathbb{R}^M$ denote the sample space of $\mathbf{X}$. The failure domain $\Omega_\mathcal{F} \subseteq \Omega$ is composed of all outcomes $\mathbf{x}$ of $\mathbf{X}$ for which the underlying system is expected to be in an undesired state (i.e., the system is expected to fail for each $\mathbf{x} \in \Omega_\mathcal{F}$). Consequently, the probability of failure $p_f$ can be obtained by the integral of the joint probability density function $f_\mathbf{X}(\mathbf{x})$ of $\mathbf{X}$ over $\Omega_\mathcal{F}$:
$$
p_f = \Pr(\mathcal{F}|\mathcal{M}) = \int_{\Omega_\mathcal{F}} f_\mathbf{X}(\mathbf{x}) \, \operatorname{d}\mathbf{x}\,,
$$ where $\Pr(\mathcal{F}|\mathcal{M})$ is used to highlight that the analysis is conditional on the assumed model $M$.
If failure of the system is expressed in terms of a so-called limit state function $g(\mathbf{x})$, the integral above can also be expressed as:
$$
p_f = \Pr(\mathcal{F}|\mathcal{M}) = \int_{g(\mathbf{x})\le 0} f_\mathbf{X}(\mathbf{x}) \, \operatorname{d}\mathbf{x}\,,
$$ where $g(\mathbf{x})\le 0$ if and only if $\mathbf{X}\in \Omega_\mathcal{F}$.
+49 (0)89 21709083
