What is the 'basic structural reliability problem'?

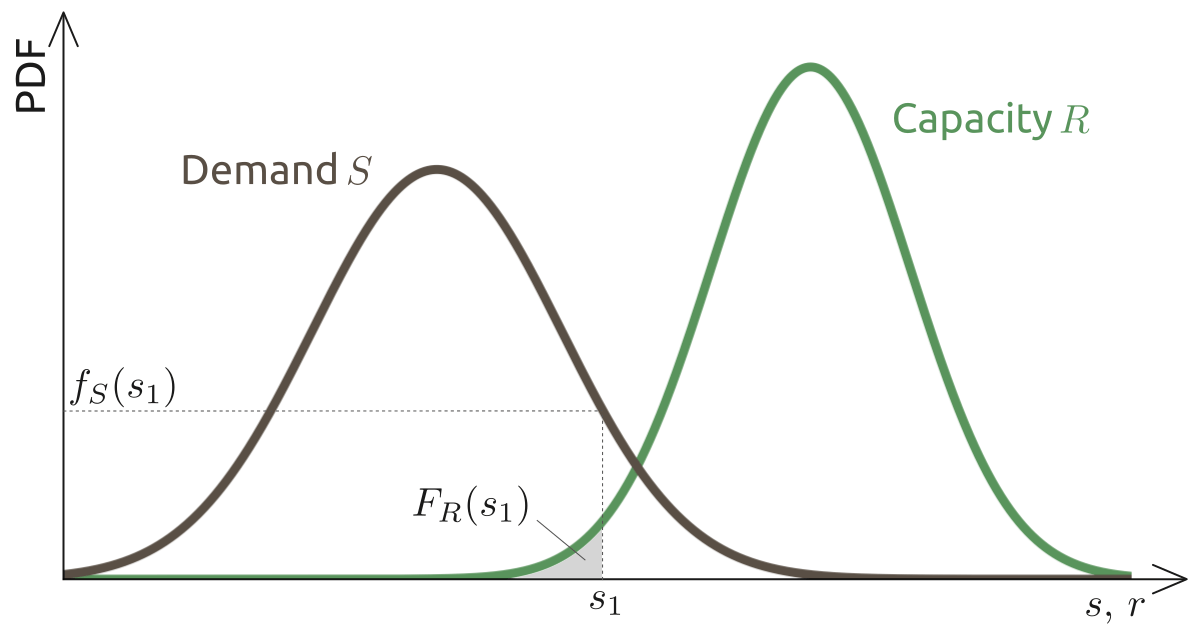
For some problems, the limit state function can be expressed as the difference between capacity $R$ and demand $S$, where failure occurs if the $R\le S$:
$$
g(R,S) = R-S\,.
$$ The corresponding problem is sometimes referred to as basic reliability problem.

For this special case, the probability of failure $p_f$ can be expressed in terms of a one-dimensional convolution integral:
$$
p_f = \Pr(\mathcal{F}) = \Pr(R\le S) = \int_S \Pr(R\le s) f_S(s) \, \operatorname{d}s = \int_S F_R(s) f_S(s) \, \operatorname{d}s \,,
$$ where $F_R(\cdot)$ denotes the CDF of $R$ and $f_S(\cdot)$ is the PDF of $S$. Equivalently, $p_f$ can also be expressed as:
$$
p_f = \Pr(\mathcal{F}) = \Pr(R\le S) = 1 - \int_R F_S(r) f_R(r) \, \operatorname{d}r \,,
$$ where $F_S(\cdot)$ denotes the CDF of $S$ and $f_R(\cdot)$ is the PDF of $R$.