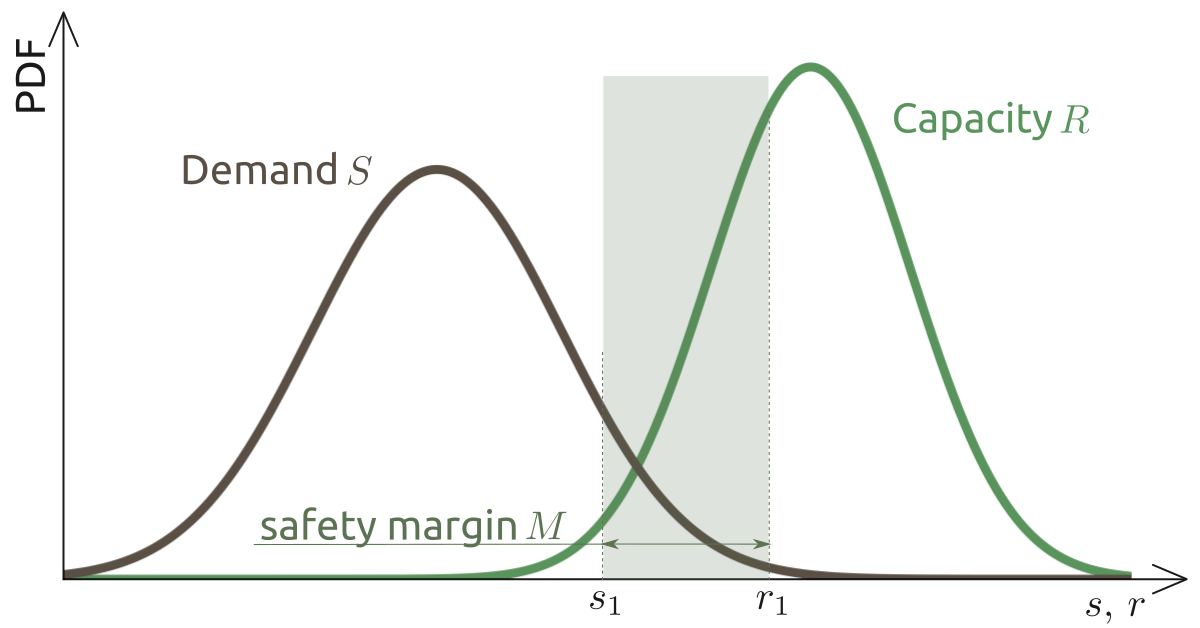
In the basic structural reliability problem, the safety margin $M$ is the difference between the capacity $R$ and the demand $S$:
$$
M=R-S\,.
$$ Note that the definition of the safety margin is equivalent to the limit state function of the basic reliability problem. Thus, the probability of failure $p_f$ can be expressed in terms of the safety margin as:
$$
p_f = \Pr(\mathcal{F}) = \Pr(M\le 0) \,.
$$
The safety margin $M$ is a function of random variables and, therefore, is a random variable itself. Looking at the statistical properties of $M$ can help to understand the problem better and learn how to improve the reliability of a structure. For example, a small coefficient of variation of $M$ indicates that increasing the mean of the resistance can be a good strategy to increase the reliability of the system. If, however, the coefficient of variation of $M$ is large, it can often be more efficient to try to decrease the uncertainty about the resistance and/or the demand.
+49 (0)89 21709083
