What is a limit state function?

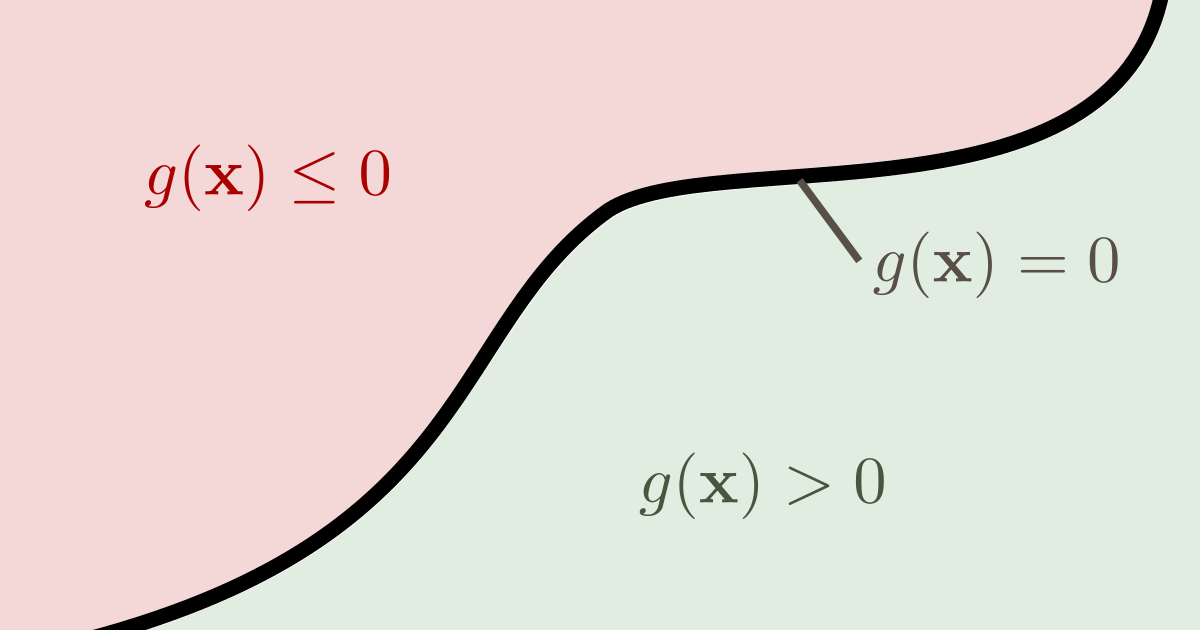
In structural reliability analysis, the limit state function (also referred to as performance function) states whether for a particular sample point $\mathbf{x}$, the expected system behavior is acceptable or undesired. More formally, let $g(\mathbf{x})$ be a function such that $g(\mathbf{x})\le 0$ if and only if the system is in an undesired state, and $g(\mathbf{x})>0$ otherwise. The probability of failure can be expressed in terms of the limit state function $g(\mathbf{x})$ as:
$$
p_f = \Pr(\mathcal{F}) = \int_{g(\mathbf{x})\le 0} f_\mathbf{X}(\mathbf{x}) \, \operatorname{d}\mathbf{x}\,,
$$ where $f_\mathbf{X}(\mathbf{x})$ is the joint probability density function of stochastic vector $\mathbf{X}$.

For the definition of the undesired system response, one typically distinguishes between the ultimate, damage and the serviceability limit-state [Melchers, 1999], where ultimate refers to at least partial collapse of the structure, and serviceability means disruption of normal use.

For some problems, the limit state function can be expressed in terms of demand $S$ and capacity $R$ of the system of interest. Failure occurs if the demand exceeds the capacity. In this case, the limit state function can be expressed as:
$$
g(\mathbf{x}) = R(\mathbf{x}) - S(\mathbf{x})\,.
$$ Note that for this simple problem, the limit-state function equals the safety margin. Problems of this type are sometimes referred to as basic structural reliability problem.

An equivalent alternative representation of the limit state function for the above example case is:
$$
g(\mathbf{x}) = 1 - \frac{S(\mathbf{x})}{R(\mathbf{x})}\,.
$$

Note that the performance of numerical methods for structural reliability analysis can depend on the particular formulation of the limit state function.