Does it make a difference whether or not a discretized Poisson process is used in Bayesian post-processing?

The answer is both "yes" and "no":

• "Yes", it makes a difference, because the posterior distributions are of different type. When learning the rate of a Poisson process, the posterior distribution is typically a Gamma distribution. When working with a discretized Poisson process and learning the probability of occurrence, the problem can be interpreted as a Monte Carlo simulation and the posterior becomes a Beta distribution.
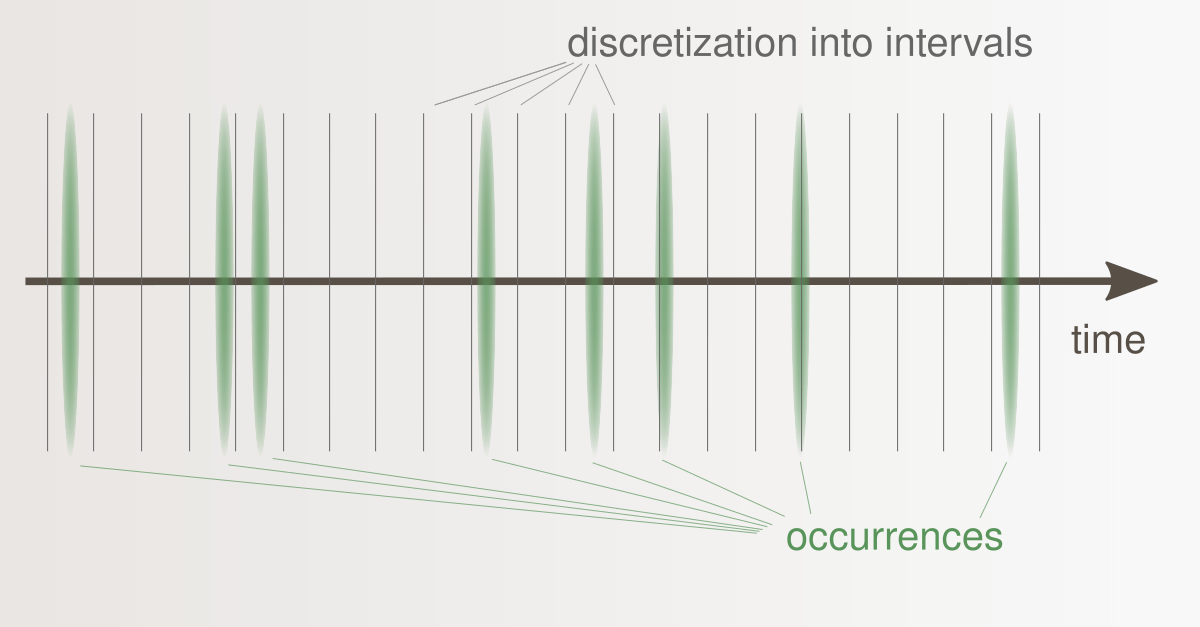
• "No", it does not make a difference if all of the following conditions are met: (i) The intervals into which the Poisson process is discretized are so small that the probability of two or more occurrences within an interval is orders of magnitude lower than the probability of one occurrence. (ii) Weakly informative (and consistent) prior distributions are used in both cases. (iii) The rate of the Poisson process of interest is sufficiently small. Sufficiently small means that if the rate is smaller than $10^{-2}$, the difference is very small; if the rate is smaller than $10^{-3}$, the difference is negligible.

Illustrative example: For example, assume an observation of a Poisson process is available where $3$ occurrences were observed within $10^4$ hours. If you directly learn the rate of the Poisson distribution using a Bayesian approach (and a weakly informative prior), the posterior mean is $4\times10^{-4}$, the $95\%$ credible interval is $7.75\times10^{-4}$ and the $99\%$ credible interval is $1.00\times10^{-3}$. If you discretize the observation into $1$ hour intervals and interpreter the problem as a Monte Carlo simulation, you get a probability of failure of $4\times10^{-4}$, with a $95\%$ credible interval of $7.75\times10^{-4}$ and a $99\%$ credible interval of $1.00\times10^{-3}$. As the probability of failure is with respect to one-hour intervals, the results of both approaches are indeed the same. ■