An appropriate prior distribution must be selected, when a Bayesian approach is used to learn the rate $\lambda$ of a Poisson process. The Gamma distribution is a conjugate prior for the problem at hand. It can be expressed in terms of a shape parameter $k^\prime$ and a rate parameter $\nu^\prime$, where both $k^\prime$ and $\nu^\prime$ must be positive.
The observations available to learn $\lambda$ are typically of the following form: We observed the Poisson process for time (or distance) $t$ and recorded $x$ occurrences of the event of interest. In this case, the posterior is a Gamma distribution with shape parameter $k^{\prime\prime} = x + k^\prime$ and rate parameter $\nu^{\prime\prime} = t + \nu^\prime$. Thus, $k^\prime$ can be interpreted as the prior number of occurrences observed within a prior interval (measured in e.g., time or distance) of length $\nu^\prime$.
Pitfalls of informative prior distributions
Most of the Poisson processes we have to handle in engineering applications can be expressed such that the rate is much closer to zero than to one. For example, the a-priori expectation of the rate could be $10^{-3}$. Does this mean we should select $k^\prime$ such that the expectation of the prior distribution becomes $10^{-3}$; i.e., $k^\prime = 10^{-3} \cdot \nu^\prime$?
No! Working with such informative priors typically allocates too much probability mass to very small values of $\lambda$. For example, with $k^\prime = 10^{-3}$ and $\nu^\prime=1.0$, the prior probability that $\lambda$ is smaller than $10^{-9}$ is above $98\%$, even though the expectation of the distribution is $10^{-3}$. With $k^\prime = 2\times10^{-3}$ and $\nu^\prime=2.0$, the prior probability that $\lambda$ is smaller than $10^{-9}$ is still above $96\%$. However, having such high confidence with respect to such small values for $\lambda$ is usually unrealistic, even though we might expect a $\lambda$ around $10^{-3}$.
One could of course decrease the coefficient of variation of the prior by increasing both $k^\prime$ and $\nu^\prime$; e.g., $k^\prime = 10^2\times10^{-3}$ and $\nu^\prime=10^2$. However, this increases the information content of the prior – and the prior probability that $\lambda$ is smaller than $10^{-9}$ is still above $20\%$ with the example at hand.
Thus, informative prior distributions need careful handling. In particular, quantile values of the employed distributions should be checked for plausibility – additional to the expected prior mean.
Selection of a weakly informative prior
A typically more suitable approach is to start with a weakly informative prior distribution. Similar to the uniform prior for MCS, the posterior should be slightly on the conservative site (for small rates, i.e., $\lambda<10^{-2}$) and should get more precise the more information becomes available.
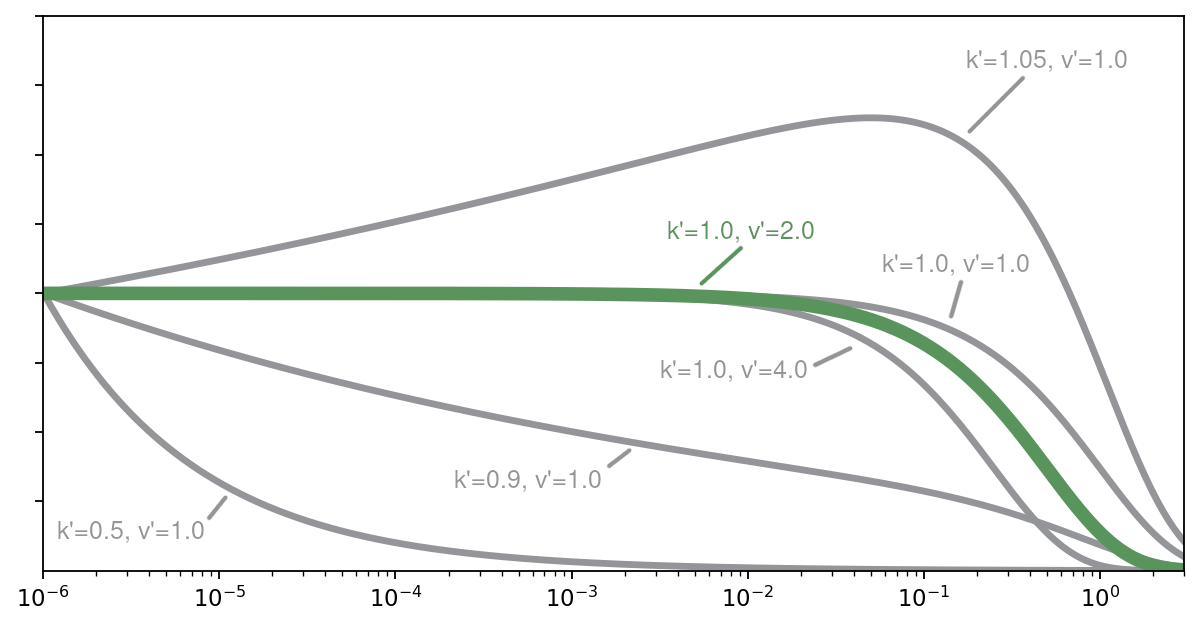
In the figure above, a selection of weakly informative prior distributions is shown. The distributions are scaled such that they have all the same value at $10^{-6}$, to facilitate the comparison of the shape of the distributions. For small values of $\lambda$ (i.e., $\lambda<10^{-2}$), we can make the following statements:
- If $k^\prime=1$, the distribution is uniform.
- If $k^\prime>1$, the density increases with increasing $\lambda$.
- If $k^\prime<1$, the density decreases with increasing $\lambda$.
The uniform density over the plausible rates (i.e., with $k^\prime=1$), combined with $\nu^\prime=2$ has properties very similar to the properties of the prior recommended for MCS. As the binomial distribution (which is the likelihood of a MCS problem) can asymptotically be approximated by a Poisson distribution, the posterior for learning the rate of a Poisson process should asymptotically converge to the posterior for MCS ($k^\prime=1$ and $\nu^\prime=2$). Therefore, selecting $k^\prime=1$ and $\nu^\prime=2$ as prior parameters seems a suitable choice.
+49 (0)89 21709083
