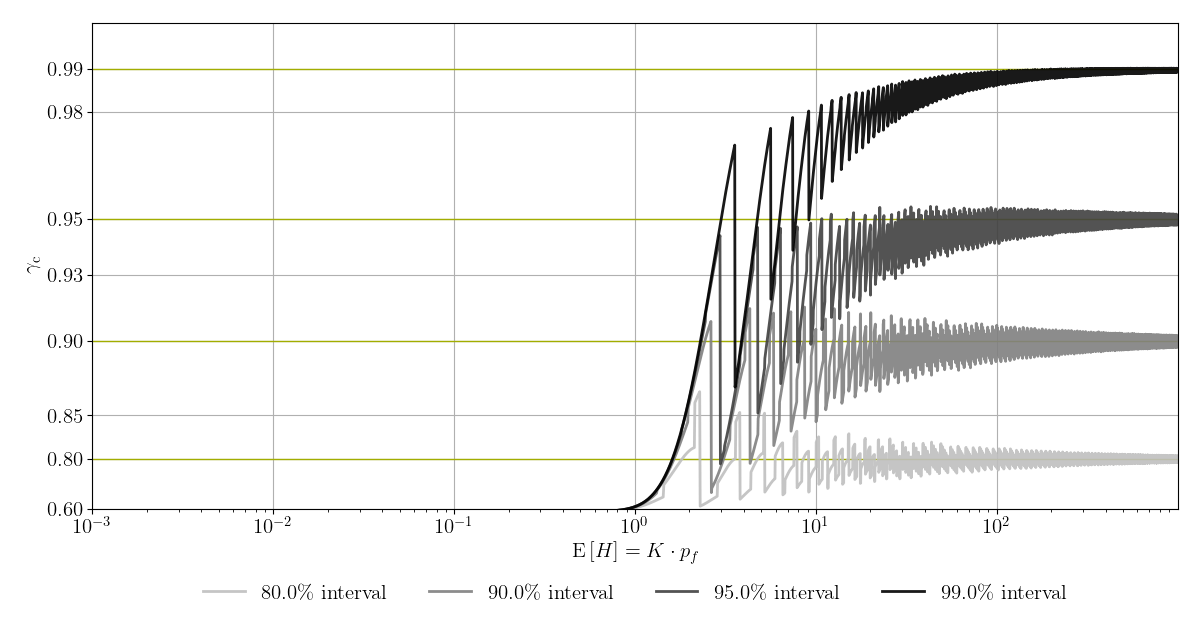
Many textbooks on structural reliability analysis use confidence intervals that are based on a Normal approximation to quantify the uncertainty about the probability of failure estimated with Monte Carlo simulation (MCS). However, the Normal distribution is a symmetric probability distribution, whereas the underlying distribution can be highly skewed. The skewness depends solely on $H$, the number of observed failure events, and not on $K$, the total number of samples in the MCS.
The image above illustrates how good the confidence intervals based on the Normal approximation perform. If the plot line is above the associated green horizontal line, the confidence interval can be considered a proper confidence interval for the particular scenario. If the plot line is below the associated green line, the confidence interval underestimates the uncertainty. Form this image above we can conclude that only if $K\cdot p_f$ is larger than $10^2$, confidence intervals based Normal on approximation provide reasonable accuracy. A condition that is rarely met in practice.
Instead of confidence intervals, we recommend using credible intervals to assess the uncertainty about the probability of failure estimated with MCS.
+49 (0)89 21709083
