Why to avoid the coefficient of variation in the context of a Monte Carlo simulation?

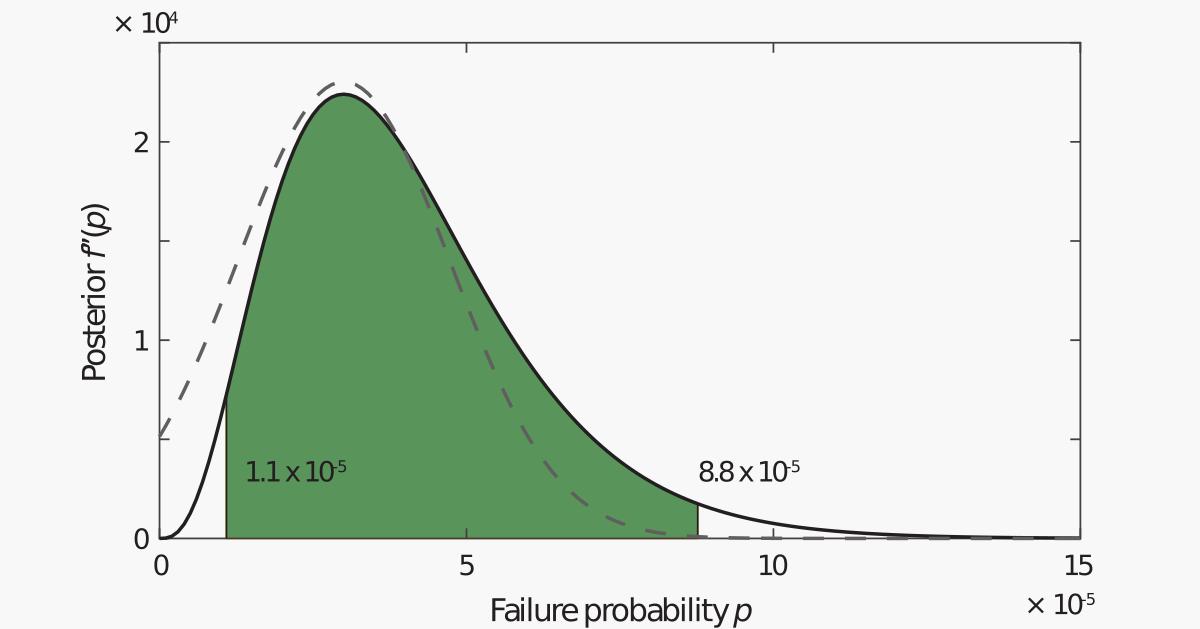
The posterior distribution $P_f|H,K$ for the probability of failure $p_f$ conditional on a conducted Monte Carlo simulation (MCS) can be highly skewed, even for a large number of samples $K$. This holds especially if the number $H$ of hits observed in the MCS is small compared to $K$. Therefore, the interpretation of the coefficient of variation can be difficult and might not be very meaningful. Credible intervals are typically a more robust measure to quantify the uncertainty about the probability of failure $p_f$.

Asymmetric shape of the posterior distribution

In the following discussion, we assume that the posterior distribution is based on the maximum entropy prior.

The mode $\Lambda$ of distribution $P_f|H,K$ is: $\Lambda={H}/{K}$. The relation of the posterior mode $\Lambda$ to the posterior mean $\mu = \operatorname{E}\left[P_f|H,K\right]$ can be stated as: $$
\tau = \frac{\Lambda}{\mu} = \frac{H}{H+1}\cdot\frac{K+2}{K} \,.
$$ If $K$ is large, the mode $\Lambda$ can be expressed relative to the mean $\mu$ as: $$
\Lambda = \mu\cdot\tau \approx \mu \cdot \frac{H}{H+1} \,.
$$ Consequently, if $H$ is small (e.g., $H<10$), the mode clearly differs from the mean. From the derivation above it is also obvious that the mode must be smaller than the mean; i.e., $\Lambda<\mu$.

Similarly, the median can be approximated as $\mu\cdot\left(H+\frac{2}{3}\right)/\left(H+1\right)$.

The skewness of the distribution $P_f|H,K$ can be approximated for large $K$ and small $H$ as $2/\sqrt{H+1}$. Under this conditions, the skew is always positive, which means that the distribution is right-skewed. Moreover, the smaller $H$, the larger the skewness is.

To summarize: For large $K$, the asymmetric shape of the posterior distribution depends solely on $H$. The smaller $H$, the more pronounced the asymmetric shape of the posterior distribution.